Prim's Algorithm

Prim's Algorithm: Building the Cheapest Network

Purpose:

Prim’s Algorithm is used to find the Minimum Spanning Tree (MST) of a connected, weighted, undirected graph.
It connects all vertices with the minimum total edge weight and no cycles.

Imagine you're designing a water pipeline to connect several houses. You want to use the least amount of pipe possible. Prim's Algorithm helps you find the shortest network to connect everything.

What Is Prim's Algorithm? (The Definition)

Prim's Algorithm is a way to find the shortest set of connections between points in a network. It starts with one point and adds the closest points until everything is connected, without creating any loops. Prims algorithm and Kruskal algorithm are based on Minimum Spanning Tree. So, we will see what is minimum spanning tree.

What is MST (Minimum Spanning Tree)?

An MST or Minimum Spanning Tree is a special kind of subgraph in a connected, weighted, undirected graph.

It connects all the vertices together with:

  • ✅ The minimum possible total edge weight

  • ✅ No cycles

  • ✅ Exactly (V - 1) edges, where V = number of vertices

How Does It Work? (The Explanation)

  1. Start Anywhere: Pick any point to begin.
  2. Find the Shortest Link: Look at all the connections from the points you've already included. Choose the shortest connection to a point you haven't included yet.
  3. Add the Link: Add that new point and the connection to your network.
  4. Repeat: Keep finding the shortest link and adding points until all points are connected.

Example: Connecting Houses with Pipes

Let's say we have houses A, B, C, and D, and the numbers are the lengths of pipes needed:

Step 1: Start at House A.

Our network starts with just house A.

Step 2: Find the Shortest Link.

  • A is connected to B (length 5) and D (length 2).
  • The shortest is A to D (length 2).

We add D and the connection A-D to our network.

   A
   |
   D

Step 3: Find the Shortest Link (Again).

  • A is connected to B (length 5).
  • D is connected to C (length 4).
  • The shortest is D to C (length 4).

We add C and the connection D-C to our network.

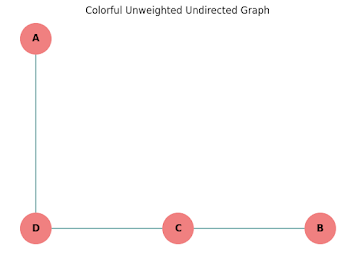
   A
   |
   D ----- C

Step 4: Find the Shortest Link (Last One).

  • A is connected to B (length 5).
  • C is connected to B (length 3).
  • The shortest is C to B (length 3).

We add B and the connection C-B to our network.

   A
   |
   D ----- C ----- B

The below is colorful graph




Step 5: We're Done!

All houses are connected.

The total length of pipe used is 2 + 4 + 3 = 9.

Why It's Useful:

It helps build the cheapest possible network for things like water pipes, roads, or computer cables.

Simple Takeaway:

Start anywhere, connect the closest thing, and keep going until everything is connected.

Feel free to comment 

Comments

Post a Comment

Popular posts from this blog

Analysis of algorithms viva questions / Interview questions - set1 /sorting algorithms

Top 10 Questions on Sorting Algorithms and Divide and Conquer Approach Top 10 Questions on Sorting Algorithms and Divide and Conquer Approach Understanding basic sorting algorithms and the divide and conquer approach is crucial for every computer science student. Below are the most frequently asked questions with answers from Module 1: Introduction to Algorithms . 1. What is Selection Sort and how does it work? Selection Sort is a comparison-based algorithm that divides the array into a sorted and unsorted part. It repeatedly selects the minimum element from the unsorted section and moves it to the beginning. Time Complexity: O(n²) Stable: No In-place: Yes 2. What are the steps involved in Insertion Sort? Insertion Sort builds the sorted array one element at a time by inserting each new element into its correct position among the previously sorted elements. Best Case: O(n) Worst Case: O(n²) Stable: Ye...
Read more

Operating System Viva questions/interview questions 2025

1. What is an Operating System? An Operating System (OS) is system software that acts as a bridge between users and computer hardware. It manages hardware resources and provides services to application software. An OS handles tasks like memory management, process scheduling, and device control. It ensures that programs and users can run smoothly without interfering with each other. Examples include Windows, Linux, macOS, and Android. The OS also provides a user interface, either graphical (GUI) or command-line (CLI). Without an OS, a computer would be unusable. It organizes files, maintains security, and manages system performance. In short, the OS is the heart of any computing device. 2. What are the main functions of an Operating System? The primary functions of an Operating System are process management, memory management, file system management, and device management. It ensures efficient execution of processes by scheduling CPU time. Memory management keeps track of ea...
Read more

Recommendation System viva questions/ Interview questions

Question 1: Can you provide an overview of the history of recommendation systems and their evolution over time? Answer: Recommendation systems have evolved significantly since their inception in the early 1990s. Initially, simple systems such as collaborative filtering and content-based filtering emerged, followed by more sophisticated techniques like matrix factorization and deep learning. The rise of e-commerce and streaming platforms in the late 1990s and early 2000s led to increased research and development in recommendation algorithms. Today, recommendation systems are ubiquitous across various domains, from e-commerce and entertainment to social media and content platforms, and continue to evolve with advancements in machine learning and artificial intelligence. Question 2: What are the main functions of a recommender system, and how do they contribute to enhancing user experience and engagement? Answer: The main functions of a recommender syste...
Read more